Papo binário - Parte 1
Os computadores vêem tudo como zeros e uns. Nesta série de tutoriais iremos “entrar” dentro dos computadores e aprender como eles funcionam.
Para se movimentar dentro dos computadores você vai precisar aprender a “falar” BINÁRIO.
BINÁRIO?!?!?
O sistema de números binários é uma maneira de escrever números usando apenas dois dígitos : 0 e 1. O sistema binário é muito útil em eletrônica, porque você pode usar esses e zeros para ficar ligado e desligado.
Como apertar um botão. Imagine que zero significa DESLIGADO e um significa LIGADO.
Objetivos:
- Entenda o que são bits e bytes e como eles se relacionam com os computadores e como as informações são processadas e armazenadas.
- Aprenda a contar na Base 2 (binária) e a converter números da Base 10 (decimal) para binário.
- Aplique o conhecimento e as habilidades acima para criar um programa exclusivo que use a contagem binária como parte integrante do programa.
Um mundo em dois dígitos
Você já deve ter ouvido os termos kilobyte (KB), Megabyte (MB), Gigabyte (GB) e Terabyte (TB), este termos normalmente são usados para se referir ao tamanho de arquivos e de espaço dos discos rígidos do computador, além é claro, da velocidade de download… Mas o que é este tal byte…
Toda informação dentro do computador , inclusive palavras e imagens, é armazenada no formato de números. Os computadores processam essa informação com dois dígitos 0 e 1.
Imagine uma luz da sala. A luz está acesa ou apagada. Você controla o estado atual da luz pressionando um interruptor que possui apenas duas possibilidades: para baixo (luz apagada) e para cima (luz acesa).
Para o computador, o zero representa um comutador ou interruptor desligado. O número 1 representa um comutador que está ligado. A contagem com zero e um se chama binária.
Um bit é um dígito binário e possui apenas dois valores possíveis, zero ou um. O valor do bit representa o estado atual de um único comutador. Se o interruptor estiver desligado, o bit terá o valor zero. Se o interruptor estiver ligado, o bit terá o valor um.
Para representar informações maiores, os bits são agrupados em sequências de 8 bits chamadas bytes.
Os computadores armazenam muita informação. São milhões e bilhões de bytes conhecidos como megabytes (mb), gigabytes (gb) e terabytes (tb).
Um byte é uma sequência de dígitos binários composta de 8 bits.
Um byte pode representar qualquer valor de 00000000 a 11111111, para um total de 256 valores possíveis diferentes.
Cada dígito em um byte pode ser considerado um comutador individual que está desativado (zero) ou ativado (um).
Os computadores modernos contam com transistores, que agrupam milhões de minúsculos comutadores em um chip menor que o seu polegar, mas as informações ainda são representadas essencialmente da mesma maneira: como uma série de zeros e uns. Usando binários, os computadores podem representar informações de maneira simples e eficiente, usando um sistema que é modelado de maneira muito eficaz em circuitos digitais.
Pode parecer confuso, porque nós viemos de um mundo decimal. Isso mesmo decimal. Temos 10 dedos em nossas mãos, então “acostumamos” a contar 10.
Deci é o prefixo original que vem do Latim decimus, que significa dezena. Assim como década significa 10 anos.

Vamos contar até 10, começando do zero.
0 1 2 3 4 5 6 7 8 9 10.
O que aconteceu quando chegamos no último dígito? Observe que usamos dois números para representar o 10.
Colocamos UM no lugar das DEZENAS e ZERO para a UNIDADE.
A mesma coisa irá ocorrer quando chegar a 99 e depois 100.
Fazemos algo semelhante no sistema binário.

- Observe a figura ao lado, primeiro, nenhum interruptor ligado. Zero
- Agora, vamos ligar o primeiro interruptor. Um
- Próximo, ligamos o segundo interruptor, e desligamos o primeiro.
- Agora, vamos ligar o primeiro interruptor novamente, mantendo o segundo ligado.
- O próximo passo, é ligar o terceiro interruptor e desligar o primeiro e o segundo
- e assim sucessivamente…
Qual seria a próxima sequencia? Se você pensou em algo assim, perfeito…

Como observamos, os computadores usam estes “interruptores” ligados e desligados para reconhecer esses ZEROS e UNS.
E como esses UNS e ZEROS se tornam números decimais? Para entender isso, primeiro vejamos o sistema decimal. Sabemos que os números são formados pelos dígitos 0 a 9, e essa é a base de 10. Lembre-se das dezenas, centenas e milhares que aprendemos nas aulas de matemática.

Observe a figura abaixo, começando pela direita temos um exemplo de representação da base 10.

Em cada posição, começando pela direita, iremos adicionar o número da posição ou índice 0, 1, 2, 3 e assim por diante…
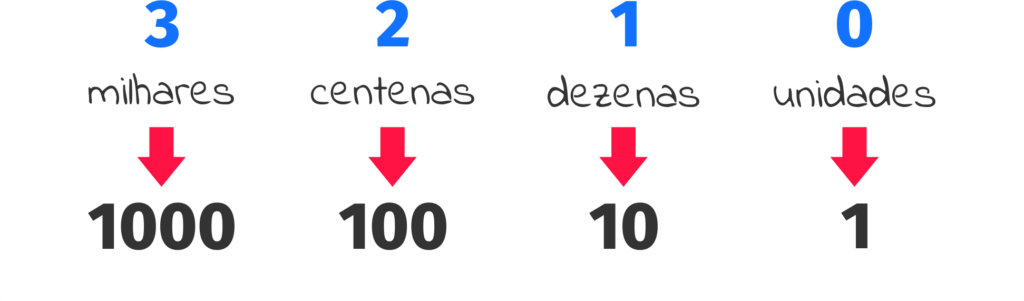
Utilizaremos este índice (0, 1, 2, 3 …) como expoente na Base 10 para obtermos as unidade, dezenas, centenas e milhares.

10 ° = 1 (todo número elevado a zero é um)
10 ¹ = 10 (sempre que o expoente for igual a 1, o resultado é igual à base)
10 ² = 10 x 10 = 100
10 ³ = 10 x 10 x 10 = 1000
Em binário é a mesma coisa, usamos estes índices (0, 1, 2, 3 …) para obter o valor na Base 2, vamos exemplificar…
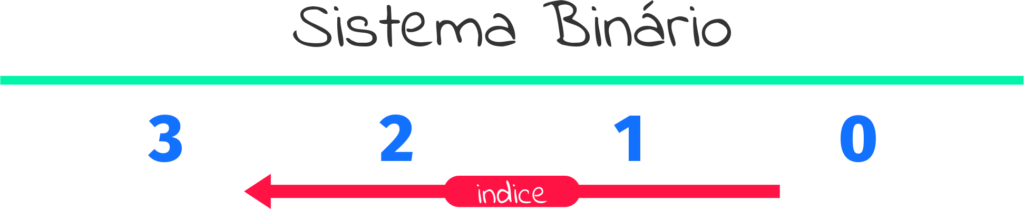
Cada posição (índice) é alocada na base de 2 para a potência desse índice…

portanto, neste caso, temos como resultado decimal 1, 2, 4 e 8…

e se eu quiser obter o valor em binário do valor decimal 9?
Lembre-se dos diferentes números em cada índice sobre os quais falamos anteriormente. Precisamos descobrir como obter 9 a partir desses números.
Temos os índices, 1, 2, 4 8 e assim por diante… para obter o valor 9, poderíamos somar 8 e 1…
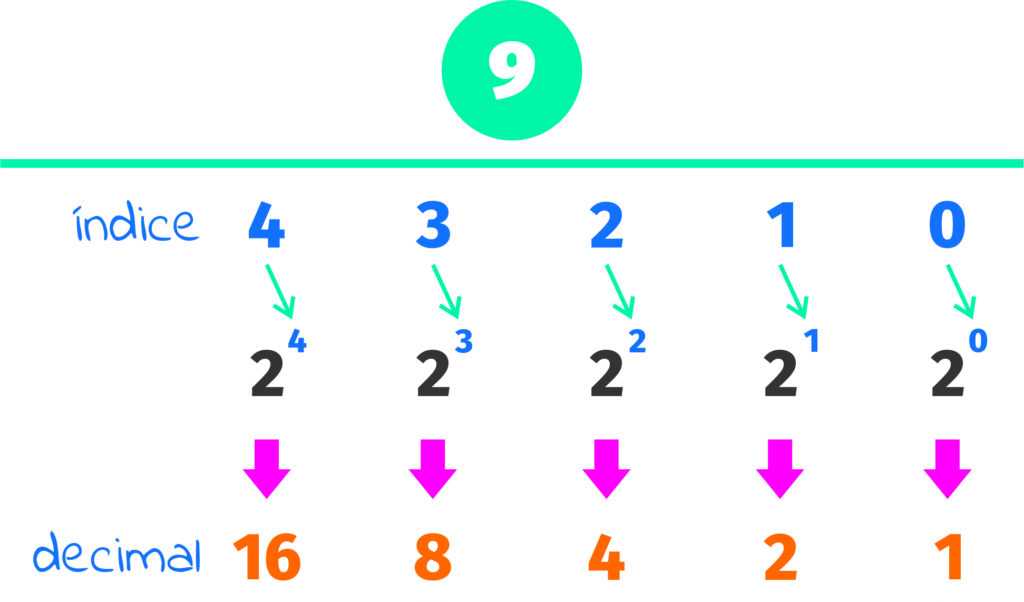
Manteremos ativados os índices 0 e 3 e desativamos os índices 1, 2, 4…
desta forma, apenas usaríamos 8 e 1 para que o número binário, obtendo, com base na sequência on e off , o binários 1001.
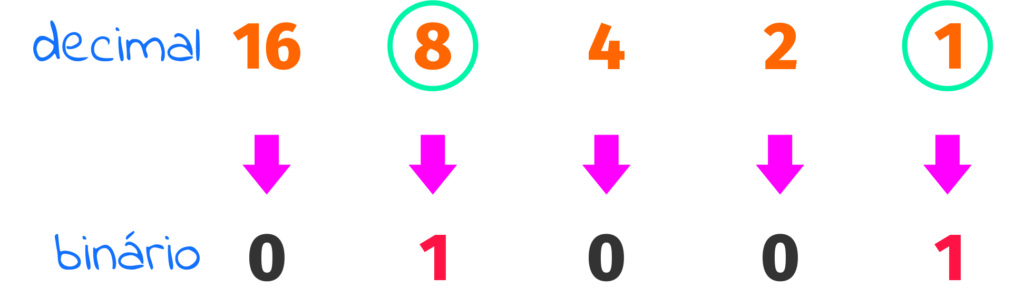
… juntos, conseguimos obter em binário o valor 9…
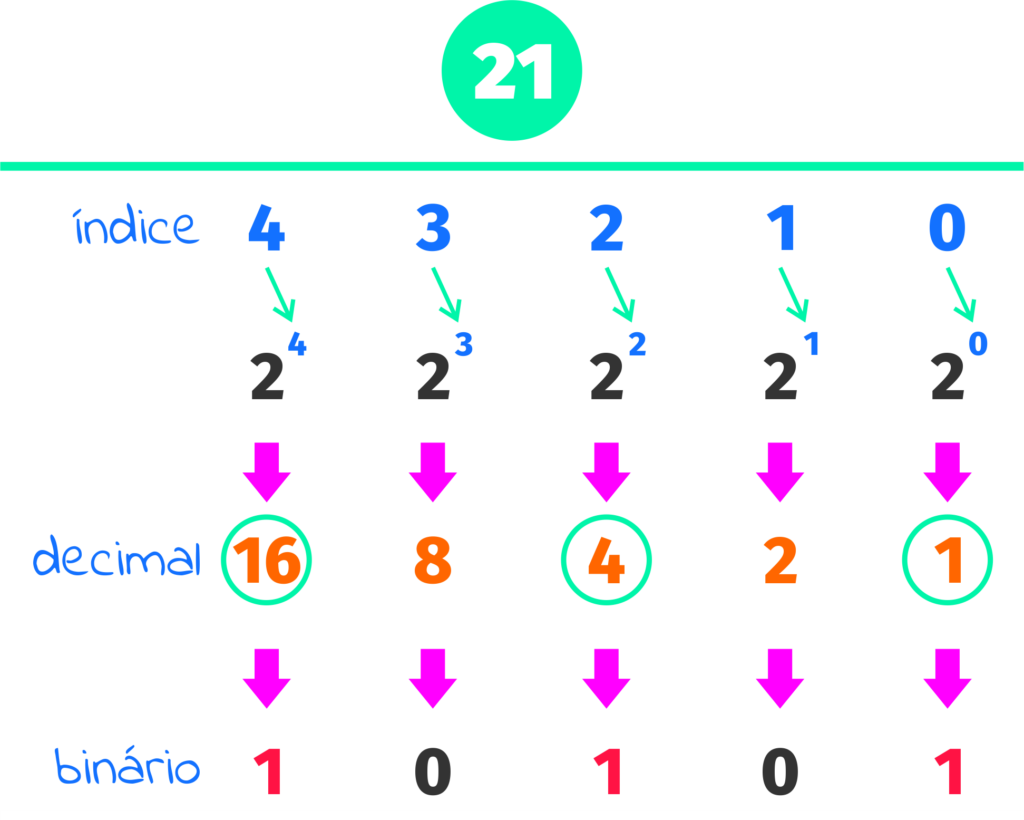
Fizemos um outro exemplo para você… analise como obter o valor binário do número decimal 21. Ligamos os índices 16, 4 e 1.
Como resultado, temos 10101 o equivalente binário para o decimal 21.

Que tal praticar um pouco… preparamos um jogo personalizado no Scratch para você testar seus conhecimentos…
Você irá ajudar o Caio a desbloquear os cadeados, convertendo os códigos decimais para códigos binários.
Você terá três vidas, então não dá para vacilar…
Clique na Bandeira Verde para iniciar.

Clique nos botões laranjas (com números) para ligar os bits (índices) necessários para a conversão…

quando estiver pronto, clique no botão ![]() para verificar se você acertou…
para verificar se você acertou…
A figura abaixo mostra um exemplo de resolução para o código é o decimal 44, ligamos o bit 32…
44 – 32 = 12
então ligamos o bit 8…
12 – 8 = 4
então ligamos o bit 4…
4 – 4 = 0
então podemos clicar no botão para verificar…![]()

#ficadica
Se você pressionar a letra s enquanto estiver jogando, você verá a soma dos valores que você selecionou no canto inferior direito, isto pode te ajudar a identificar se você está no caminho certo de sua resposta. 😉
