Papo binário - Parte 3
Lógica desplugada
Neste tutorial, você irá explorar o conceito de lógica, matemática e números binários experimentando um card game. Ao final você encontra um link para fazer o download dos materiais para você imprimir e se divertir.
Game 1: Solucionando histórias enigmáticas
Este jogo consiste na solução de nove histórias com estruturas lógicas, distribuindo as cartas dentro de um tabuleiro. Para encontrar a solução, você terá 9 cards (três personagens, três pets e três brinquedos) e 9 cards de desafios além do tabuleiro.
O tabuleiro é igual ao da imagem ao lado, nele você irá distribuir os cards de acordo com o card de desafio que você escolher.
Na primeira coluna você irá colocar os cards com os personagens (Caio, Kelly e Ed).
Na segunda coluna é o espaço para você colocar os cards dos animais de estimação, temos o canguru, o koala e o ornitorrinco.
A terceira coluna receberá os cards ilustrados com os brinquedos, a bicicleta, patins e o skate.



Solucionando um desafio:
Kelly quer ver o ornitorrinco.
Se Ed foi passear de patins, ele viu um ornitorrinco.
Caio foi andar de skate.
Ed viu um coala.
Quem viu o canguru?
Quem foi andar de bicicleta?
Solução:
Quem viu o canguru?
Caio
Quem foi andar de bicicleta?
Ed

Game 2: Quadrados Mágicos (3x3)
Este é um card game muito interessante, um quadrado mágico que possibilita uma reflexão de fácil entendimento. São três linhas e três colunas, no qual devem-se dispor os números de 1 a 9, de modo que a soma em cada linha, coluna e diagonal seja 15.
Todas as oito soluções dos Quadrados Mágicos devem obedecer esta regra : o jogador deverá organizar as cartas numeradas, de 1 a 9, de maneira que a soma dos
números, no sentido horizontal, vertical e das
duas diagonais, seja sempre 15.
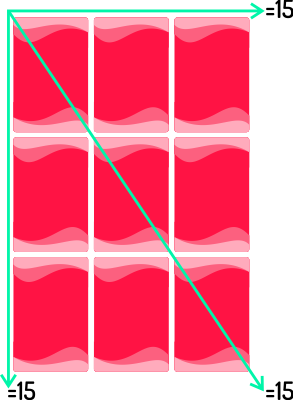
Entendendo a solução dos quadrados mágicos.
1. Temos 9 algarismos a serem distribuídos no quadrado: 1, 2, 3, 4, 5, 6, 7, 8 e 9.
2. Entre os números 1 a 9 temos: 5 números ímpares e 4 números pares.
3. As possíveis combinações com três números são:
a) par+par+par = par
b) par+par+ímpar = ímpar
c) par+ímpar+ímpar = par
d) ímpar+ímpar+ímpar=ímpar
Para isto iremos começar analisando as diagonais.
5. O número que irá ocupar o centro do quadrado mágico merece uma atenção especial, pois ele estará presente em quatro das oito somas. Analise a opção b do item 3. Se o número do centro for par, os outros dois números de cada diagonal devem ser: um par e outro ímpar

6. Isto nos leva a duas situações
1ª Situação – Esta forma de distribuir os números exige um número ímpar na primeira linha, para que a soma seja ímpar, conforme observamos na opção b do ítem 3, o que vai deixar a terceira linha com três números pares


2ª Situação – Nos levaria a uma mesma solução, porém distribuindo os números em uma rotação anti-horária em relação à 1ª solução.

7. Cabe agora, tentar manter um número ímpar no centro do quadrado mágico. Como vimos no ítem 3, há duas possíveis maneiras de preencher as diagonais do quadrado de forma que as somas sejam ímpares. Neste caso temos quatro possíveis soluções possíveis.
1ª Situação – Observe que esta não é a solução adequada, pois pelo descrito na opção c do item 3, se complementarmos as demais casas com números pares, as somas das linhas e colunas seriam todas pares.

2ª Situação – Esta também não seria uma solução, pois seguindo as regras possíveis no item 3, precisaríamos preencher as casas com números pares. Porém, só temos 4 pares de 1 a 9. Para esta solução precisaríamos de 6.

3ª Situação – Observe que esta solução é uma rotação anti-horária da situação 2, portanto também não é uma solução.

4ª Situação – Esta pode ser uma solução, pois bateria preencher as casas vazias com ímpares. Com isto definimos que o centro é um número ímpar. Nosso próximo passo é analisar as combinações usando os valores de 1 a 9.

8. Ainda continuamos nossa análise para identificar as possíveis combinações para as diagonais. As possíveis combinações que resultam em 15, contendo dois pares e um ímpar são:
- 1+8+6
- 2+5+8
- 2+6+7
- 2+9+4
- 3+4+8
- 4+5+6

O próximo passo é distribuir os números restantes de forma a obter o resultado 15 nas somas.
Estas são todas as possíveis soluções para o quadrado mágico 3×3:
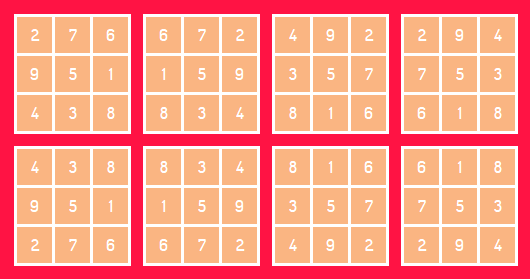
Fonte: GONÇALVES, A. O. A lógica dos quadrados mágicos 3×3. Educação Matemática em Revista, n. 20/21, p. 10-12, dez. 2006.
Você pode fazer o dowload do PDF da folha de atividade para imprimir e usar clicando no botão abaixo.
