Diversão com Operações Lógicas - Parte 4
O pseudocódigo de Pedra-Papel-Tesoura v.2.0
Na lição constante ou variável construímos um contador de pontos para jogos, usando como exemplo de uso o jogo: Pedra-Papel-Tesoura, resolvemos turbinar o contador de pontos, juntando ele ao próprio jogo Pedra-Papel-Tesoura, já que ele utiliza padrões de decisão que estamos estudando. Você poderá jogar contra o micro:bit, jogar contra um amigo ou amiga, jogar contra outro micro:bit, isso mesmo, depois de você enviar o programa para seu micro:bit você pode jogar contra o simulador, micro:bit físico contra micro:bit virtual.

Pense no que você quer que seu programa faça, elabore o pseudocódigo.
Para este jogo usamos três objetos: Pedra, Papel e Tesoura.
Iremos registrar o pontos marcados pelo Jogador A (você), Jogador B (oponente) e empates.
Ao agitar o micro:bit será escolhido o seu objeto pelo micro:bit;
Verifique, visualmente, o objeto escolhido por seu adversário;
Se seu objeto for papel e do adversário for pedra marque pontuação para o Jogador A e escreva “A”, senão se seu objeto for pedra e do adversário for tesoura marque pontuação para o jogador A e escreva “A”, senão se seu objeto for tesoura e do adversário for papel marque pontuação para o jogador A e escreva “A”, senão se seu objeto for igual ao do adversário registre o empate e escreva “E”, senão marque pontuação para o jogador B e escreva “B”.
Alguns lembretes importantes:
precisaremos armazenar a sua pontuação (Jogador A), de seu oponentes (Jogador B), e também a quantidade de vezes que ocorre o empate.
Precisaremos também de uma variável para armazenar um número aleatório que corresponda aos objetos: Pedra (1) Papel (2) Tesoura (3).
Pseudocódigo
- Quando iniciar a tela deverá está limpa, sem nenhum tipo de informação;
- Quando iniciar, as variáveis devem iniciar com 0;
- Agite para o micro:bit escolher um número aleatório que será correspondente a um de seus três objetos;
- Leia o objeto escolhido;
- Usuário observa o objeto do adversário;
- SE seu objeto for papel e do adversário for pedra pressione o botão A e mostre “A“; (você ganhou)
- SENÃO SE seu objeto for pedra e do adversário for tesoura pressione o botão A e mostre “A“;(você ganhou)
- SENÃO SE seu objeto for tesoura e do adversário for papel pressione o botão A e mostre “A“;(você ganhou)
- SENÃO SE seu objeto for igual ao do adversário pressione A+B e mostra “E“;(empate)
- SENÃO pressione o botão B e mostre “B” (você perdeu);
- Para visualizar os resultados o micro:bit deverá ser colocado com o logotipo para cima.

Matemática em toda parte
As vezes aprendemos a programação de jogos e deixamos de observar tudo que está ao redor desta construção de um jogo tão simples como PEDRA | PAPEL | TESOURA.
Nestas atividades, além do aprendizado de operações lógicas, estamos aprendendo sobre a teoria das probabilidades, que é um ramo importante da matemática com muitas aplicações práticas nas ciências físicas, médicas, biológicas e políticas.
Além disso, a probabilidade também está presente em atividades como jogos de tabuleiro, esportes, jogos de parque infantil, parque de diversões, festas e desafios. É a matemática em toda parte.
Esta é uma introdução e exploração de jogos simples, que envolvem a probabilidade utilizando os jogos de mão. Iremos a seguir apresentar algumas coisas interessantes que talvez você ainda não tenha parado para pensar quando joga PEDRA | PAPEL | TESOURA.
PROBABILIDADE
Probabilidade… a probabilidade é a chance de que um determinado evento ocorra.
Você já parou pensar em questões como:
Como é que os jogos funcionam?
O que fazem esses jogos serem divertidos?
Que papel a probabilidade poderia desempenhar em jogos de um torneio?
Dois jogadores disputando PEDRA, PAPEL e TESOURA, quais as chances do parceiro mostrar PEDRA, ou TESOURA…
Se você nunca jogou PEDRA, PAPEL e TESOURA, a pontuação do jogo é a seguinte: a pedra quebra a tesoura, então “pedra” bate “tesoura”; o papel cobre a rocha, por isso, “papel” bate “pedra”; e a tesoura corta o papel, de modo que “tesoura” bate “papel”. Se os parceiros mostram o mesmo símbolo, considera-se um empate. Desenhamos um diagrama para determinar os possíveis resultados do jogo.
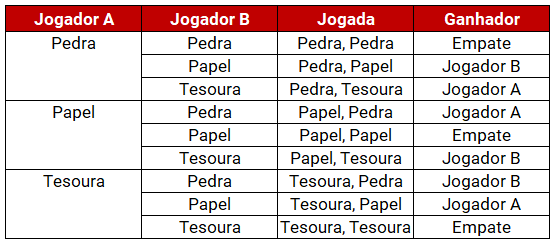
Observando a tabela, quantos resultados possíveis tem o jogo?
3 x 3 = 9
Quantas vezes o Jogador A ganha?
Três vezes, então a probabilidade deste jogador ganhar é 3/9. A mesma coisa ocorre para o Jogador B e para Empates.
Este é um jogo justo ou injusto?
Se ambos os jogadores têm igual
probabilidade de ganhar em qualquer rodada, então ele é considerado um jogo
justo; se eles têm probabilidades desiguais de ganhar, então ele é considerado
injusto. Então, este é um jogo justo.
Você já imaginou, este mesmo jogo sendo disputado por 3 jogadores?
Passaríamos a ter 27 resultados, ou 3 x 3 x 3 possibilidades.
Experimente montar a mesma tabela que fizemos para dois jogadores, só que agora com três, será que ainda teríamos o mesmo nível de igualdade?
